 Mort il y a plus de 400 ans, le Père Christophorus Clavius a toujours été considéré comme l’initiateur de la tradition scientifique et particulièrement mathématique de la Compagnie de Jésus.
Mort il y a plus de 400 ans, le Père Christophorus Clavius a toujours été considéré comme l’initiateur de la tradition scientifique et particulièrement mathématique de la Compagnie de Jésus.
Pourquoi le lendemain du 4 octobre 1582, fête de S. François d’Assise devint le 15 octobre, supprimant ainsi dix jours du calendrier ? Pourquoi est-il dit que S. Thérèse d’Avila est morte « dans la nuit du 4 au 15 octobre 1582 » ? Pourquoi le Père jésuite Clavius a pu justifier la suppression de 10 jours du calendrier romain ?
Le 6 février 1612, mourait à Rome Christophorus Clavius, figure-clé du début de la tradition scientifique de la Compagnie. Clavius était né à Bamberg, Allemagne, en 1537 et il manifesta sans cesse clairement son attachement à sa cité natale en ajoutant toujours cette référence à son nom dans ses livres (Clavius Bambergensis). Nous ne connaissons pas exactement son nom de famille en allemand, qui pouvait être Klau ou Schlussel, mais qui apparut toujours en sa forme latinisée. Nous n’avons guère plus de certitudes sur ses premières études, jusqu’à ce qu’il soit reçu dans la Compagnie par saint Ignace lui-même à Rome en 1555, bien que l’on suppose qu’il avait étudié au collège tenu par les jésuites à Bamberg. En 1556 il étudia la philosophie à Coimbra, où il observa une éclipse du soleil en 1559, premier contact avec son intérêt pour l’astronomie.

Il retourna à Rome en 1560 pour terminer ses études de philosophie et commencer ses études de théologie. Il fut ordonné prêtre en 1564. Son intérêt pour les mathématiques a dû s’éveiller tôt, car il remplaça dès 1567 l’espagnol Baltasar Torres (1481-1561) dans la chaire de mathématiques, qu’il occupa jusqu’en 1595. Pendant les dernières années de sa vie et jusqu’à sa mort en 1612, il continua à rester actif, supervisant les éditions de ses livres et se maintenant attentif aux nouvelles observations et aux propositions du domaine de l’astronomie, dues à Copernic, Tycho Brahe, Galilée et Kepler.
Clavius fut fondamentalement un grand professeur, et les jésuites mathématiciens et astronomes postérieurs l’ont toujours considéré comme l’initiateur de la tradition scientifique et particulièrement mathématique de la Compagnie. Directement ou indirectement à travers leurs livres, les mathématiciens jésuites de première génération se reconnaissaient comme disciples de Clavius, éprouvant à son égard une profonde révérence et se référant à lui comme à «notre Clavius».
 Sa production fut très vaste, comportant 23 livres publiés entre 1570 et 1612. Douze d’entre eux sont des manuels d’arithmétique, de géométrie et d’algèbre, trois commentaires des ouvrages de géométrie d’Euclide et de Théodose et d’astronomie de Sacrobosco, et six livres concernent la défense de la réforme grégorienne du calendrier. L’année de sa mort (1612) furent publiées ses œuvres complètes (Opera Mathematica) en cinq volumes. Sa production couvrait toutes les disciplines mathématiques de son époque en une collection de manuels qui restèrent en usage pendant de longues années.
Sa production fut très vaste, comportant 23 livres publiés entre 1570 et 1612. Douze d’entre eux sont des manuels d’arithmétique, de géométrie et d’algèbre, trois commentaires des ouvrages de géométrie d’Euclide et de Théodose et d’astronomie de Sacrobosco, et six livres concernent la défense de la réforme grégorienne du calendrier. L’année de sa mort (1612) furent publiées ses œuvres complètes (Opera Mathematica) en cinq volumes. Sa production couvrait toutes les disciplines mathématiques de son époque en une collection de manuels qui restèrent en usage pendant de longues années.
Parmi ses ouvrages, il convient de détacher en premier lieu l’édition et le commentaire des 15 livres d’Euclide (Euclidis elementarum libri XV commentarius, 1574, le Commentaire des 15 livres des Eléments d’Euclide : les livres 14 et 15 attribués à Euclide sont dus à des auteurs grecs postérieurs) qui lui valut le titre de «l’Euclide de notre temps», avec trois éditions datant du vivant de l’auteur, la dernière datant de 1691. Dans le prologue de cette œuvre, Clavius fait voir l’importance de la géométrie pour la compréhension de la nature, dès lors que le monde en sa totalité est le résultat de la géométrie. Par cette considération Clavius se rapproche des courants de la «nouvelle science» qui exigeait la connaissance des mathématiques pour décrire les phénomènes naturels. Son innovation la plus importante consiste peut-être en l’addition de solutions numériques aux démonstrations géométriques. Ce livre se convertit pour de nombreuses années en manuel de géométrie de la majorité des collèges jésuites, et marqua de son empreinte l’importance donnée dans ces établissements à la géométrie dans l’enseignement des mathématiques.

A ce livre s’en ajoutent deux autres d’arithmétique et de géométrie pratiques. Arithmetica Practica, en particulier, bénéficia d’un très large accueil concrétisé par 25 éditions jusqu’en 1738, dont 10 en latin et 15 en italien, témoignant de la qualité de Clavius comme excellent professeur et vulgarisateur de l’arithmétique. Cette popularité se devait d’une part à la clarté du texte, et de l’autre à la nécessité, à cette époque, d’un ouvrage de ce style pour les calculs indispensables au commerce ainsi qu’à l’industrie naissante. Dans ce livre Clavius introduisit certaines nouveautés comme l’usage du point inscrit à la fin des nombres pour les séparer, et à l’intérieur pour séparer les milliers dans les grands nombres. C’est de cette proposition que dérive l’usage actuel du point pour séparer les décimales.
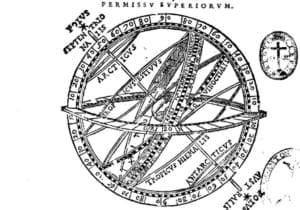
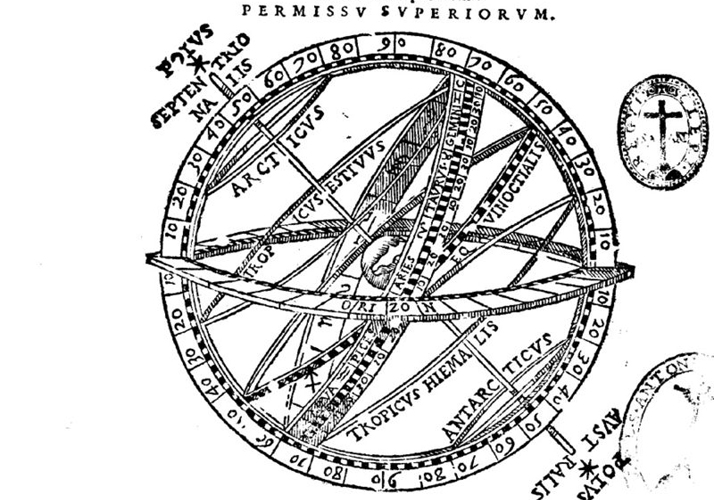
Le point focal de l’œuvre de Clavius en astronomie est occupé par son commentaire du livre Tractatus de sphaera (Traité de la sphère) de Johannes Sacrobosco (John Holywood), anglais, professeur à Paris au XIIIe siècle, qui présente sous une forme simplifiée l’astronomie de Ptolémée et fut très populaire au Moyen-Age. Claude Ptolémée avait composé à Alexandrie au IIe siècle sa grande synthèse de l’astronomie, où il rassemblait tout le savoir astronomique de l’antiquité grecque en un ouvrage connu plus tard sous son titre arabe, Almageste, et qui passa ensuite en Europe en sa traduction latine au Xlle siècle.
Clavius se sert de ce livre (In sphaeram bannis de Sacrobosco commentarius, 1570, Commentaire du livre de la sphère de Jean de Sacrobosco), qui connut six éditions du vivant de son auteur, la dernière en 1611, pour présenter une vision de l’astronomie de son temps. Ses commentaires sont, en fait, beaucoup plus étendus que le texte original de Sacrobosco. Dans son travail, Clavius présente une astronomie géocentrique ptolémaïque fidèle à la réalité physique des sphères célestes autour de la Terre qui occupe le centre de l’univers, les excentriques et les épicycles. Clavius est donc resté fidèle à la défense traditionnelle de l’immobilité de la Terre et de sa position centrale dans l’univers, conformément à la physique d’Aristote et à l’interprétation littérale de la Bible, laquelle en certains passages mentionne le mouvement du soleil et la stabilité de la Terre. Toutefois, d’une édition à l’autre de ses ouvrages, Clavius introduit petit à petit les nouveaux apports astronomiques; c’est ainsi que dans l’édition de 1581, Clavius reconnaît la valeur astronomique de l’œuvre de Copernic, qu’il appelle «l’illustre restaurateur de l’astronomie» bien qu’il n’en vint jamais à accepter son système.
Tout en reconnaissant la grande valeur de l’œuvre de Copernic en tant que source d’observations, de tables et de calculs, Clavius considérait que l’opinion de Ptolémée méritait d’être préférée aux «inventions» de Copernic. Dans la dernière édition de 1611, Clavius mentionne les découvertes de Galilée au télescope en 1609 et 1610, les observations nouvelles dont les novas de 1570, 1600 et 1604 et la comète de 1577 qui montraient que les cieux n’étaient pas incorruptibles, contrairement à la doctrine aristotélicienne, et les phases de Vénus et les satellites de Jupiter qui montraient que tout ne tournait pas autour de la Terre. Faisant le compte de tout cela, Clavius commente qu’une réforme des orbites célestes est indispensable.
L’inexactitude du calendrier julien, instauré dans tout l’Empire romain par Jules César en l’an 45 av. J-C., puis observé dans l’Occident chrétien, avait depuis longtemps mis en évidence la nécessité d’une réforme, justifiée avant tout par la variation de la date prévue pour l’équinoxe du printemps, qui s’écartait de plusieurs jours du 21 mars, ce qui avait une retombée sur la date de célébration de Pâques. La renommée de Clavius porta le pape Grégoire XIII à le rappeler à faire partie de la commission chargée d’examiner la réforme que l’italien feu Luigi Giglio (Aloysius Lilius) avait proposée et qui avait finalement été acceptée.

La réforme, proclamée par le Pape Grégoire XIII en 1582, comportait la suppression de 10 jours du calendrier entre le 4 et le 15 octobre de cette année-là. Clavius fut chargé d’expliquer et de défendre la réforme dans un gros ouvrage publié en 1595 (Romani calendarii a Gregorio XIII restitui explicatio, Explication du calendrier romain rétabli par Grégoire XIII) auquel suivit la publication de cinq travaux en plus, commandés par le pape Clément VIII et qui défendaient la réforme contre ses adversaires, surtout originaires du camp protestant.
Cette participation à la réforme du calendrier ne fit que rehausser davantage encore la réputation de Clavius, surtout au-delà du milieu jésuite. Le tombeau de Grégoire XIII à la Basilique Saint-Pierre comporte un bas-relief sur lequel apparaît un clerc offrant au Pape un livre sur la réforme du calendrier et l’on suppose qu’il s’agit de Clavius.
Si cette supposition devait s’avérer exacte, Clavius serait le seul jésuite représenté dans la basilique Saint Pierre, outre saint Ignace.
Clavius commença à participer à la composition de la Ratio studiorum avec des propositions sur renseignement des mathématiques en 1580. Sa position, que nous pouvons appeler militante, en faveur de ces enseignements est concrétisée en divers écrits. Clavius propose une série de recommandations pratiques aptes à permettre une pédagogie des mathématiques, qui tende à donner aux mathématiques dans l’enseignement de la philosophie autant d’importance qu’à la philosophie naturelle. Cela supposait une vision nouvelle des programmes de philosophie, ouvrant en ceux-ci une voie d’entrée à la science moderne que l’on commençait à proposer avec sa formulation mathématique et sa base dans l’expérimentation. Clavius insiste surtout sur la nécessité des mathématiques pour traiter des thèmes de la physique, dès lors que «par ignorance des mathématiques certains professeurs commettaient de nombreuses et graves erreurs»; il affirme que «sans les mathématiques la philosophie naturelle est boiteuse».
Il en avait conscience, la philosophie de la nature, alors ancrée sur les énoncés de la doctrine aristotélicienne, ne pouvait avancer que par l’application des mathématiques et il voyait clairement comment le progrès de la science allait être lié à l’application des mathématiques à l’étude des phénomènes naturels, exactement tel que commençaient à le faire les initiateurs de la science moderne. En conséquence de quoi Clavius pensait que les étudiants jésuites ne pouvaient rester en marge de ce mouvement.
 Dans les textes des deux premières versions de la Ratio de 1586 et 1591, l’influence de Clavius est facile à voir. On y vante les avantages de l’étude des mathématiques, «puisque sans cela manquerait à toute notre académie un grand ornement,» et l’on ne manque pas de mentionner l’utilité de cette étude pour la société et pour l’Église. La pénurie des bons professeurs de mathématiques est dénoncée et, pour les former, est proposé un programme spécial de trois ans destiné à un groupe réduit de jeunes jésuites de diverses provinces qui feraient preuve du talent voulu. L’espoir est que sortent de cette «académie» d’illustres mathématiciens qui dissémineraient leur savoir dans toutes les provinces de la Compagnie. Dans le texte de 1591, il est établi – comme dans le texte antérieur – que l’on explique à tous les élèves de deuxième année de philosophie les Éléments d’Euclide, géographie et astronomie, et il est de nouveau proposé que l’on établisse une académie de mathématiques (academia rerum mathematicarum) pour les quelques-uns qui auraient témoigné d’un intérêt particulier pour ces études après avoir achevé leurs années de philosophie.
Dans les textes des deux premières versions de la Ratio de 1586 et 1591, l’influence de Clavius est facile à voir. On y vante les avantages de l’étude des mathématiques, «puisque sans cela manquerait à toute notre académie un grand ornement,» et l’on ne manque pas de mentionner l’utilité de cette étude pour la société et pour l’Église. La pénurie des bons professeurs de mathématiques est dénoncée et, pour les former, est proposé un programme spécial de trois ans destiné à un groupe réduit de jeunes jésuites de diverses provinces qui feraient preuve du talent voulu. L’espoir est que sortent de cette «académie» d’illustres mathématiciens qui dissémineraient leur savoir dans toutes les provinces de la Compagnie. Dans le texte de 1591, il est établi – comme dans le texte antérieur – que l’on explique à tous les élèves de deuxième année de philosophie les Éléments d’Euclide, géographie et astronomie, et il est de nouveau proposé que l’on établisse une académie de mathématiques (academia rerum mathematicarum) pour les quelques-uns qui auraient témoigné d’un intérêt particulier pour ces études après avoir achevé leurs années de philosophie.
Dans la version définitive de la Ratio de 1599, la mention des mathématiques est plus brève et ne cite pas explicitement «l’académie de mathématiques», bien que la référence à l’étude privée plus poussée destinée à un groupe retreint d’étudiants y soit maintenue. Lors des révisions des versions antérieures, des commentaires étaient parvenus à Rome sur la difficulté d’enseigner les mathématiques dans certaines provinces; Clavius s’était donc vu dans l’obligation d’adopter cette solution de compromis dans le texte final, en retrait sur son désir premier.
Clavius, pendant son professorat au Collège romain, forma une école de mathématiques qui servit de modèle à tous les collèges de la Compagnie. Sur les 625 collèges — à peu près — que la Compagnie entretenait en Europe au début du XVIIIe siècle, 95 avaient une chaire de mathématiques, dont la qualité était reconnue de toute part.
Agustin Udias, sj
Traduction de Anne Stainier
Laisser un commentaire
Vous devez vous connecter pour publier un commentaire.